Note

We are facing some issues in rendering Latex mathematical equations on this page.Refer opening this blog in Colab (button on the top right) to solve rendering issues.

What is Probability

It is useful to start with defining what probability is. There are three main categories:

1. Classical probability

$Pr(X=x) = \\frac{\\text{# x outcomes}}{\\text{# possible outcomes}}\$

Classical probability is an assessment of possible outcomes of elementary events. Elementary events are assumed to be equally likely

2. Frequentist probability

$Pr(X=x) = \\lim_{n \\rightarrow \\infty} \\frac{\\text{# times x has occurred}}{\\text{# independent and identical trials}}\$

This interpretation considers probability to be the relative frequency \"in the long run\" of outcomes.

3. Subjective probability

Subjective probability is a measure of one's uncertainty in the value of $X\$. It characterizes the state of knowledge regarding some unknown quantity using probability.In simple terms,An event's probability is the degree of belief that the event will occur. Subjective probabilities are personal judgments based on all of the assessor's previous experience relevant to the situation at hand.

It is not associated with long-term frequencies nor with equal-probability events. For example:

X = the true prevalence of diabetes in Bengaluru is < 15,
X = the blood type of the person sitting next to you is type A
X = it is raining in Bengaluru,India

We will cover on this more in our future blogs where we delve into Frequentist vs Bayesian Approach to Statistics but for now we will consider Frequentist approach and will talk about Probabilites as frequency.

General Defintion which I like:

Probability is the measure of certainity of an event taking place.
The world we see around us is full of phenomena we perceive as random or unpredictable. We aim to model this phenomena as outcomes of some experiment. The outcomes are a result of sample space and subsets of sample space are called events. The events will be assigned a probability a number between 0 and 1 that expresses how likely the event is to occur.

Elements of Probabilty

Sample Space(Ω)

Sets whose elements describe the outcomes of the experiment in which we are interested.In simpler terms ,it is the set of all outcomes in an experiment. In the case of an experiment on the month,a person's birthday falls, an obvious choice for the sample space is

Ω = {Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec}

Events(F)

Subsets of the sample space are called events.We say that an event A occurs if the outcome of the experiment is an element of the set A. For eg. In the birthday experiment we can ask for the outcomes that correspond to a long month, i.e., a month with 31 days.

This is the event L = {Jan, Mar, May, Jul, Aug, Oct, Dec}.

Lets define an another event R - that corresponds to the months that have the letter r in their (full) name (so R = {Jan, Feb, Mar, Apr, Sep, Oct, Nov, Dec}

1. Intersection of two events (L ∩ R) i.e if both L and R occur
   Long months that contain the letter r are : {Jan, Mar, Oct, Dec} 
2. Union of two events (L U R) i.e atleast one of the events L and R occurs.
3. Disjoint or Mutually Exclusive (L ∩ R) = ∅ i.e L and R have no outcomes in common i.e they cannot occur at the same time.

Probability Measure(P)

To express how likely it is that an event occurs, we will assign a probability to each event.Since each event has to be assigned a probability, we speak about Probability function.

This probabilty function has to satisfy the following properties: If we define a probability function P on a finite sample space Ω assigns to each event A in Ω denoting P(A) as Probability that A occurs then:

P(A)>= 0 for all A belonging to F
P(Ω) = 1 i.e outcome of the experiment is always an element of the sample space
P(A U B) = P(A) + P(B) if A and B are disjoint

OR and AND Operations
Given two events A and B ,that are not disjoint:

$P(A or B) = P(A) + P(B) - P(A and B)$ or can be denoted as $ P(A U B) = P(A) + P(B) - P(A ∩ B) $

Products of sample spaces

Suppose we throw a coin two times. What is the sample space associated with this new experiment? It is clear that it should be the set Ω = {H, T } × {H, T } = {(H, H), (H, T ), (T, H), (T, T )}

General Notation Two experiments with sample spaces Ω1 and Ω2 then the combined experiment has as its sample space the set Ω = Ω 1 × Ω 2.
If Ω 1 has r elements and Ω 2 has s elements, then Ω 1 × Ω 2 has rs elements

Conditional Probabilty and Independence

Knowing that an event has occurred sometimes forces us to reassess the probability of another event; the new probability is the conditional probability.

Lets pick up our previous example:
Birthday Months Ω = {Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec}
Born in a long month - L = {Jan, Mar, May, Jul, Aug, Oct, Dec}
Born in a month with the letter 'r' - R ={Jan, Feb, Mar, Apr, Sep, Oct, Nov, Dec}

Hence, P(L) = $7/12$ and P(R) = $8/12$

No if we get to know that a person was born in a long month and wanted to find out whether he was born in a month with the letter 'r' . In this case , we will filter out some of the outcomes of a sample space belonging to R which is not possible now.It cannot be February, April, June, September, or November as thay are not in our long months set.

So our answer would be out of 7 possible outcomes in R , now only 4 is possible. We call this the conditional probability of R given L i.e P(R/L) = $4/7$

Note

P(R/L) is not same as P(R ∩ L) as P(R ∩ L) = $4/12$

A good way to get an intuition on this conept would be to think like P(R | L) is the proportion that P(R ∩ L) is of P(L) or in simple terms it means finding which fraction of the probability of L is also in the event R

For better intuition and visualisation refer the below tree diagram tounderstand the concept

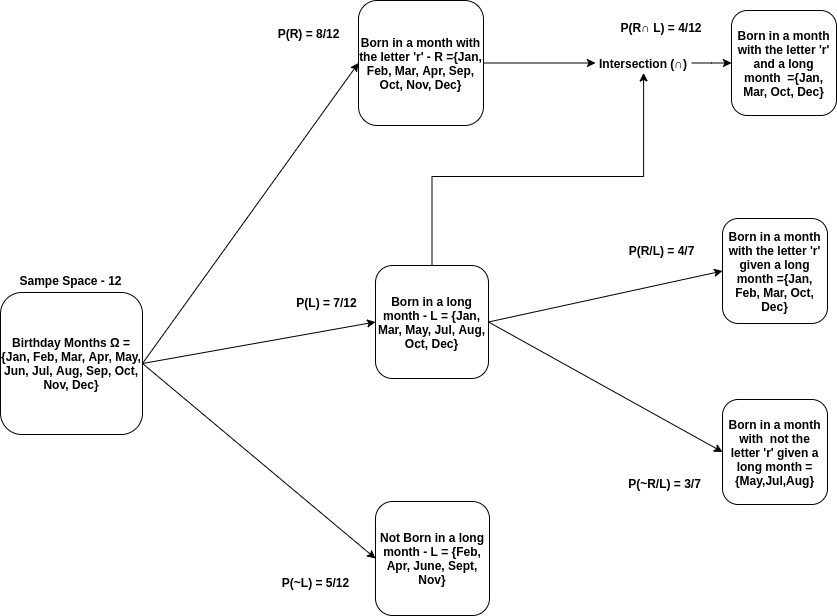
The conditional probability of R given L is given by:

$P(R | L)$ = $\\frac{P(R ∩ L)}{P(L)}\$ provided P(L) > 0

where:

$P(R | L)$ - Conditional Probability

$P(R ∩ L)$ - Joint Probability

$P(L)$ - Marginal Probability

Multiplication Rule

Using the above derived rule of Conditional Probability and multiplying both sides by P(L)

$P(R ∩ L) = P(R | L) . P(L)\$

Computing the probability of R ∩ L can hence be decomposed into two parts, computing P(L) and P(R | L) separately.Here we are conditioning on L.

Note
Conditioning can help to make computations easier, but it matters how it is applied. To compute P(R ∩ L) we may condition on L to get $P(R ∩ L) = P(R | L) · P(L)$ or we may condition on R and get $P(R ∩ L) = P(L | R) · P(R)$. Both ways are valid, but often one of $P(R | L)$ and $P(L | A)$ is easy and the other is not.

Let us take an example and validate our argument. Suppose we meet two arbitrarily chosen people. What is the probability their birthdays i.e P(B₂) are different?

Whatever the birthday of the first person is, there is only one day the second person cannot pick as birthday, so: $P(B_{2}) = 1 − \\frac{1}{365}\$

Simple right. But what if we extend this problem to 3 person or say n numbers? This is where Conditional Probabilty becomes handy.

Lets take an example with 3 persons
Probability that 3 persons birthdays i.e P(B₃) are different
The event B₃ can be seen as the intersection of the event B₂ i.e. “the first two have different birthdays,” with event A₃ i.e “the third person has a birthday that does not coincide with that of one of the first two persons.”

or $P(B_3 ) = P(A_3 ∩ B_2 ) = P(A_3 | B_2 )P(B_2 )$

where $P(A_3 | B_2 ) = (1 − \\frac{2}{365})\$ and

and $P(B_2) = (1-\\frac{1}{365})\$

Hence, $P(B_3) = (1 − \\frac{2}{365}). (1-\\frac{1}{365})\$

So you can see , we now have a framwork which can be applied for n numbers as well.

$P(B_n) = (1-\\frac{n-1}{365})..(1 − \\frac{2}{365}). (1-\\frac{1}{365})\$

This same problem can be solved if we try conditioning on $A_3$ like

$P(B_3 ) = P(A_3 ∩ B_2 ) = P(B_2 | A_3 )P(A_3 )$
but just trying to understand the conditional probability P(B 2 | A 3 ) already is confusing: The probability that the first two persons’ birthdays differ given that the third person’s birthday does not coincide with the birthday of one of the first two . . . ?

Takeaway
Conditioning should lead to easier probabilities; if not, it is probably the wrong approach

Law of Total Probability and Bayes' Rule

Lets start with an example again

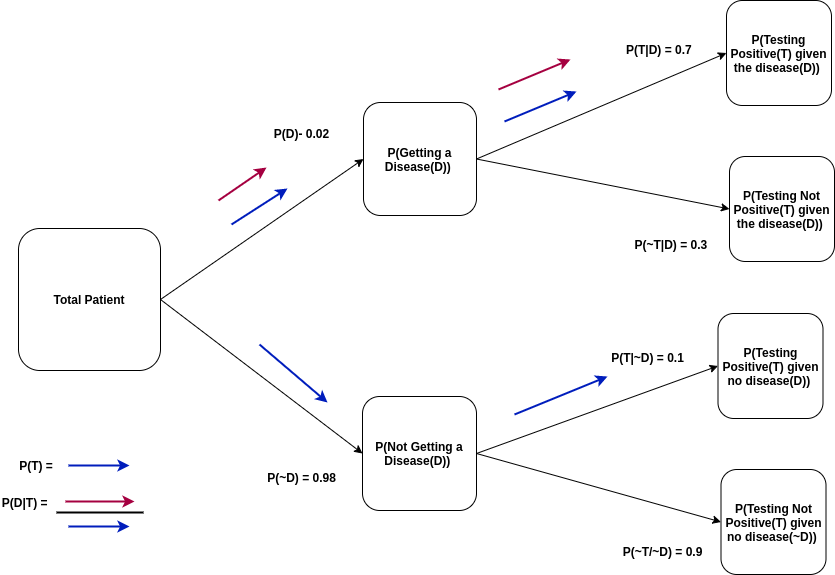
Problem Statement
We have the following data:
An infected patient has a 70% chance of testing positive and a healthy patient just 10% chance of testing positive for the disease.Probability of having a diesase is 0.02.Determine the Probability of an arbitrary patient testing positive to the disease?

P(Testing Positive(T) given the disease(D)) or $P(T|D) = 0.7 $

P(Testing Positive(T) given no disease(D^c)) or $P(T|D^c)) = 0.1 $

P(Getting a Disease(D)) or $P(D) = 0.02$

P(Testing Positive) or $P(T) = ?$

Solution
Patient testing positive is either infected or it is not. So all in all we have these two scearios.

$T = (T ∩ D) ∪ (T ∩ D^c )$
i.e $P(T ) = P(T ∩ D) + P(T ∩ D^c )$

and we know from Condtionality

$P(T ∩ D) = P(T | D) · P(D)$

$P(T ∩ D^c ) = P(T | D^c ) · P(D^c )$

Putting the values in the equation:

$P(T ) = 0.02 · 0.70 + (1 − 0.02) · 0.10 = 0.112$

This is an application of the law of total probability: computing a probability through conditioning on several disjoint events that make up the whole sample space (in this case two).

If we generalize this..

The law of total Probability

Suppose $C_1 , C_2 , . . . , C_m$ are disjoint events such that $C_1 ∪ C_2 ∪ · · · ∪ C_m = Ω.$ The probability of an arbitrary event A can be expressed as:

$P(A) = P(A | C_1 )P(C_1 ) + P(A | C_2 )P(C_2 ) + · · · + P(A | C_m )P(C_m )$

Bayes’ rule.

Another follow up question we can ask in the above problem statement is.. If a patient tests positive; what is the probability it really has the disease i.e $P(D|T)$ ?

Solution

$P(D|T) = \\frac{P(D ∩ T)}{P(T)}\ or \\frac{P(T ∩ D)}{P(T)}\$

$P(D|T) = \\frac{P(T | D) · P(D)}{P(T | D) · P(D) + P(T | D^c ) · P(D^c )}\$ = 0.125

Similary we can do for $P(D|T_c)$ which will be equal to 0.0068

What we have just seen is known as Bayes’ rule.

Suppose the events C_1 , C_2 , . . . , C_m are disjoint and C_1 ∪ C_2 ∪ · · · ∪ C_m = Ω. The conditional probability of C_i , given an arbitrary event A, can be expressed as:

$P(C_i | A) = \\frac{P(A | C_i ) · P(C_i )}{P(A | C_1 )P(C_1 ) + P(A | C_2 )P(C_2 ) + · · · + P(A | C_m )P(C_m )}\$

Independence

Consider three probabilities from the previous section:

$P(B) = 0.02$ i.e If we know nothing about a person, we would say that there is a 2% chance it is infected

$P(B | T ) = 0.125$ i.e if we know it tested positive, we can say there is a 12.5% chance the person is infected

$P(B | T_c ) = 0.0068.$ if it tested negative, there is only a 0.68% chance

We see that the two events are related in some way: the probability of D depends on whether T occurs.

Imagine the opposite: the test is useless.

Whether the person is infected is unrelated to the outcome of the test, and knowing the outcome of the test does not change our probability of D: $P(D | T ) = P(D)$. In this case we would call D independent of T

Defintion An event A is called independent of B if $P(A | B) = P(A)$

Let us see how our earlier formula changes in the light of Independence

$P(A ∩ B) = P(A | B)P(B) = P(A) P(B)$

$P(B | A) = \\frac{P(A ∩ B)}{P(A)}\ = \\frac{P(A).P(B)}{P(A)}\$ = P(B)

To show that A and B are independent it suffices to prove just one of the following:

$P(A | B) = P(A)$
$P(B | A) = P(B)$
$P(A ∩ B) = P(A) P(B)$

If one of these statements holds, all of them are true. If two events are not independent, they are called dependent.

Recall the example of birthday events L “born in a long month” and R “born in a month with the letter r.” Let H be the event “born in the first half of the year,” so $P(H) = 1/2.$ Also, $P(H | R) = 1/2$. So H and R are independent.

Extending it to two or more events

Independence of two or more events. Events $A_1 , A_2 , . . . , A_m$ are called independent if:

$P(A_1 ∩ A_2 ∩ · · · ∩ A_m ) = P(A_1 ) P(A_2 ) · · · P(A_m )$

Note - Independence for three events A, B, and C is not the same as: A and B are independent; B and C are independent; and A and C are independent.

Marginal Probablity in Matrix Form

Lets take an example and see how does it fit in a matrix form

Let $P(X_1 = 0) = 3/4$ and $P(X_1 = 1) = 1/4$ . Given $P(X_2 = 1 | X_1= 0) = 1/3$ $P(X_2 = 1 | X_1= 1) = 0$. Then $P(X_2 = 0 | X_1 = 0) = 2/3$ , $P(X_2 = 0 | X_1 = 1) = 1$

In Matrix Form

$X_1$ : \begin{bmatrix} 3/4 & 1/4 \end{bmatrix}

$X_1X_2$ : where $X_1$ is the row and $X_2$ is the column in the matrix with row and column headers as [ 0,1 ] \begin{bmatrix} 2/3 & 1/3 \\ 0 & 1 \end{bmatrix}

We can obtain the expression for $P(X_2)$ easily using matrix notation

which is $P(X_2) = $$\sum$$P(X_1 )P(X_2 | X_1 )$

$ X_2$ : \begin{bmatrix} 3/4 & 1/4 \end{bmatrix}

Test Yourself

Explain Probability in your terms?
What are Axioms of Probability?
Define Sample Space and Events?
How does a sample space change when we combine multiple experiments as one experiment?
Intuition on Conditional Probability?
Expression of Conditional Probability?
Difference between Conditional Probability vs Joint Probability and Marginal Probability?
Understanding different expressions like : $P(A | B) , P(A ∩ B),P(A U B), P(A), P(AB)$
Intuition on Baye's rule ?
Intuition on Independence Condition and changes in the follwing expressions in case of independence $P(A ∩ B), P(B | A), P(A | B)$ ?

Questions

If we perform an experiment with outcomes 1 (success) and 0 (failure) five times, and we consider the event A “exactly one experiment was a success,.Find P(A) given P(Getting outcome 1) = p

Answer
$5(1 − p)^4 p$

What is the probability of the event B “exactly two experiments were successful”?

Answer
$10(1 − p)^3 p^2$

Suppose an experiment in a laboratory is repeated every day of the week until it is successful, the probability of success being p. The first experiment is started on a Monday. What is the probability that the series ends on the next Sunday.

Answer
$p(1 − p)^6$