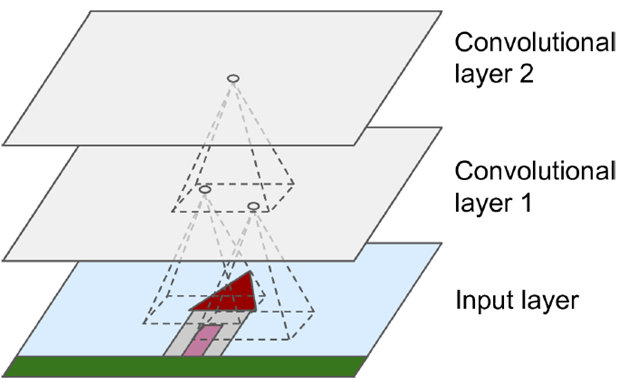
Convolutions in Deep Neural Network
An in depth introduction to different concepts in Convolution
- Why CNN and not Regular Neural Nets
- Convolution
- Convolution over Volume
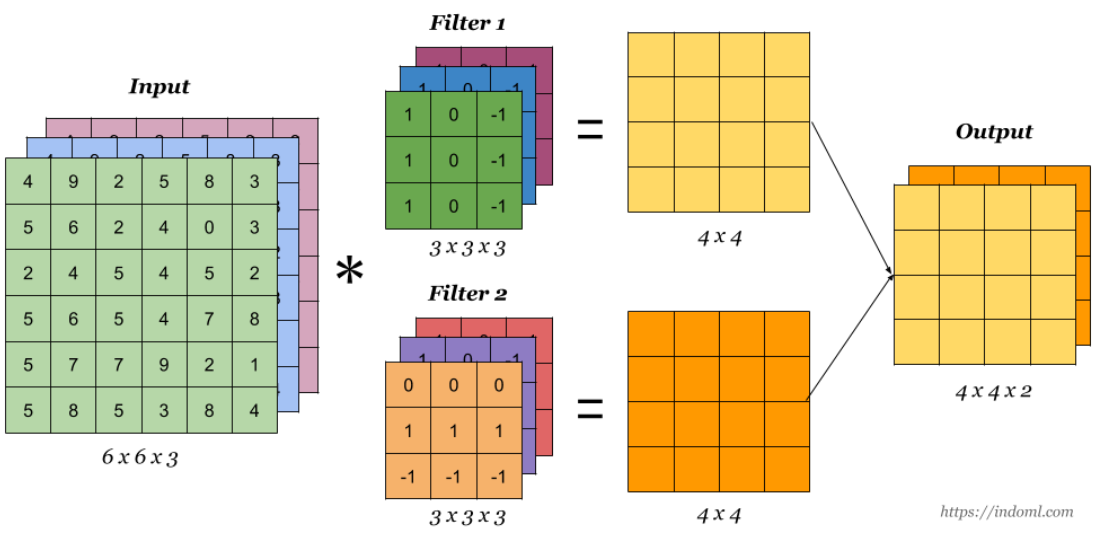
- Convolution Operation with Multiple Filters
- General Representation
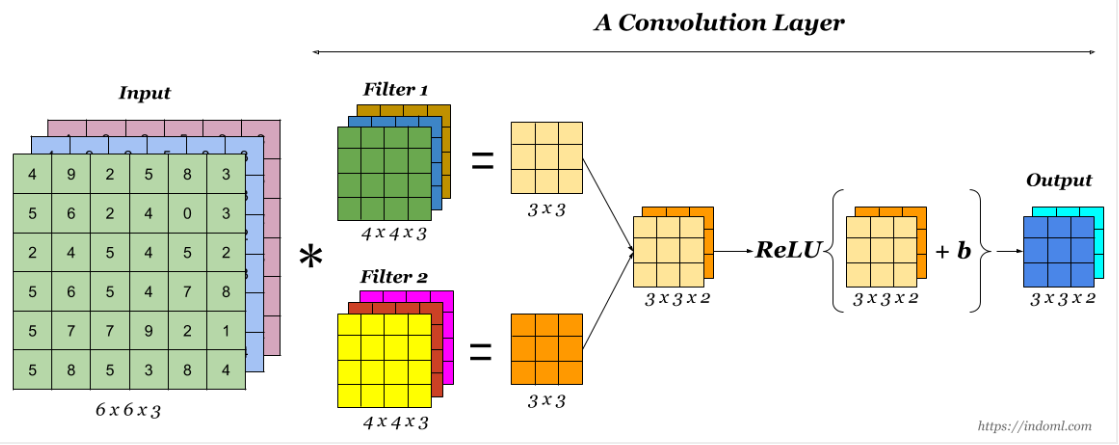
- One Convolution layer
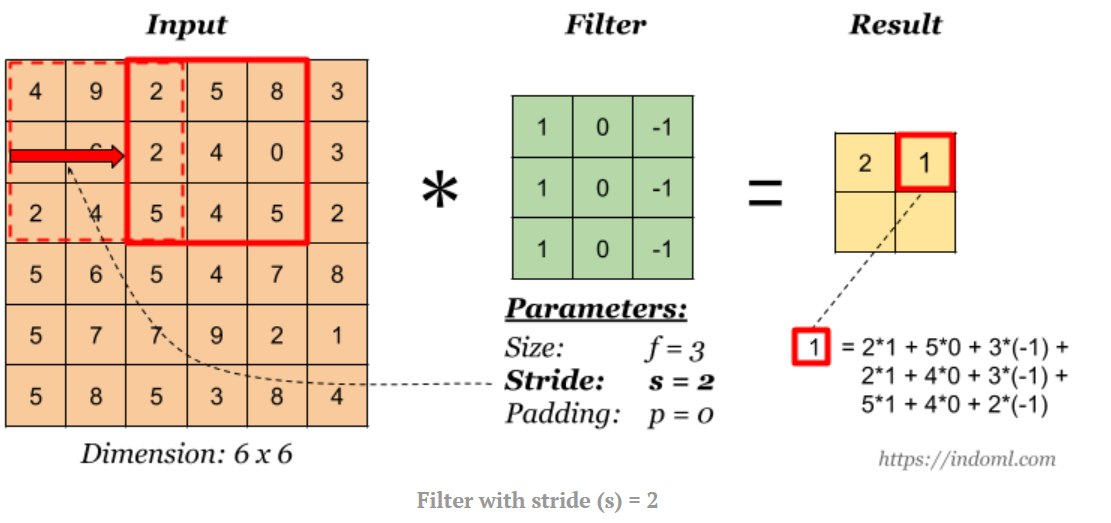
- Strides
- Padding
- Pooling
- General Representation-Updated
- Examples
- 1 x 1 Convolution
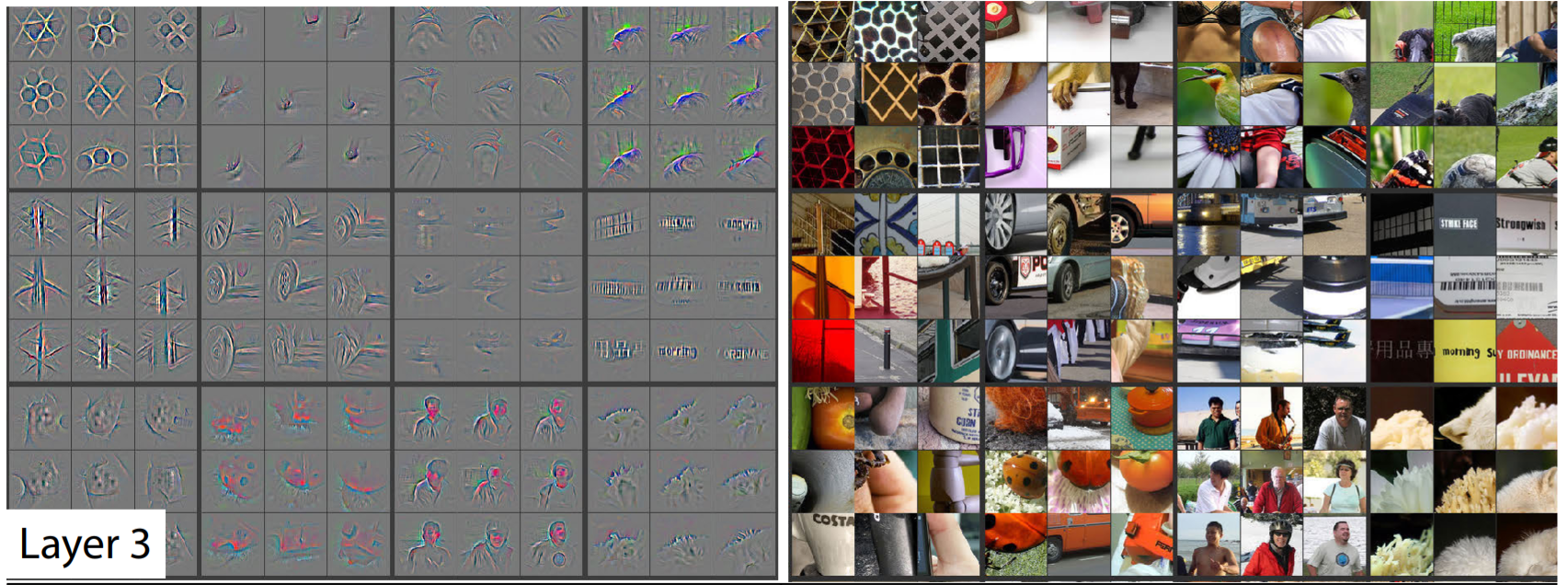
- Receptive Field
- Things to remember
- References
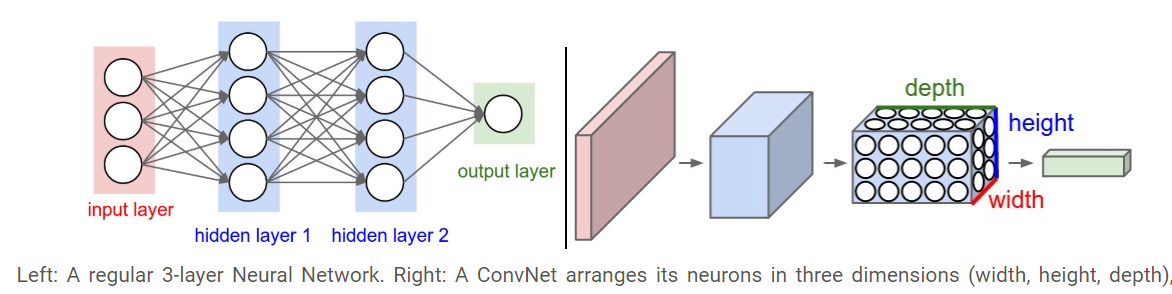
Why CNN and not Regular Neural Nets
1. Regular Neural Nets don’t scale well to full images
In MNIST dataset,images are only of size 28x28x1 (28 wide, 28 high, 1 color channels), so a single fully-connected neuron in a first hidden layer of a regular Neural Network would have 28x28x1 = 786 weights. This amount still seems manageable,
But what if we move to larger images.
For example, an image of more respectable size, e.g. 200x200x3, would lead to neurons that have 200x200x3 = 120,000 weights. Moreover, we would almost certainly want to have several such neurons, so the parameters would add up quickly! Clearly, this full connectivity is wasteful and the huge number of parameters would quickly lead to overfitting.
2.Parameter Sharing
A feature detector that is useful in one part of the image is probably useful in another part of the image.Thus CNN are good in capturing translation invariance.
Sparsity of connections In each layer,each output value depends only on a small number of inputs.This makes CNN networks easy to train on smaller training datasets and is less prone to overfitting.
2.3D volumes of neurons. Convolutional Neural Networks take advantage of the fact that the input consists of images and they constrain the architecture in a more sensible way. In particular, unlike a regular Neural Network, the layers of a ConvNet have neurons arranged in 3 dimensions: width, height, depth.
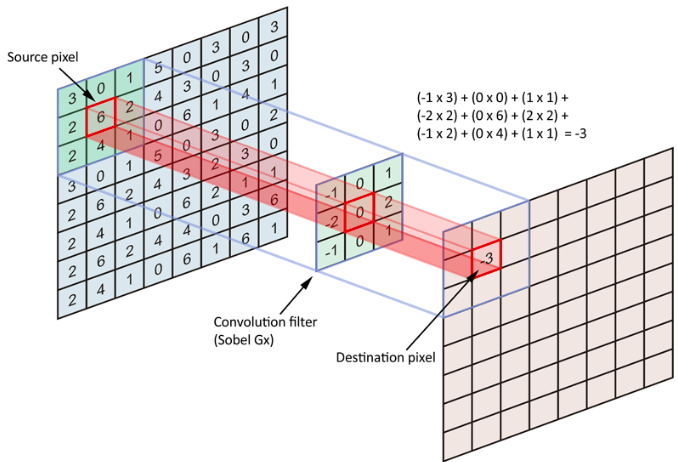
Convolution
In purely mathematical terms, convolution is a function derived from two given functions by integration which expresses how the shape of one is modified by the other.
However we are interested in understanding the actual convolution operation in the context of neural networks.
An intuitive understanding of Convolution
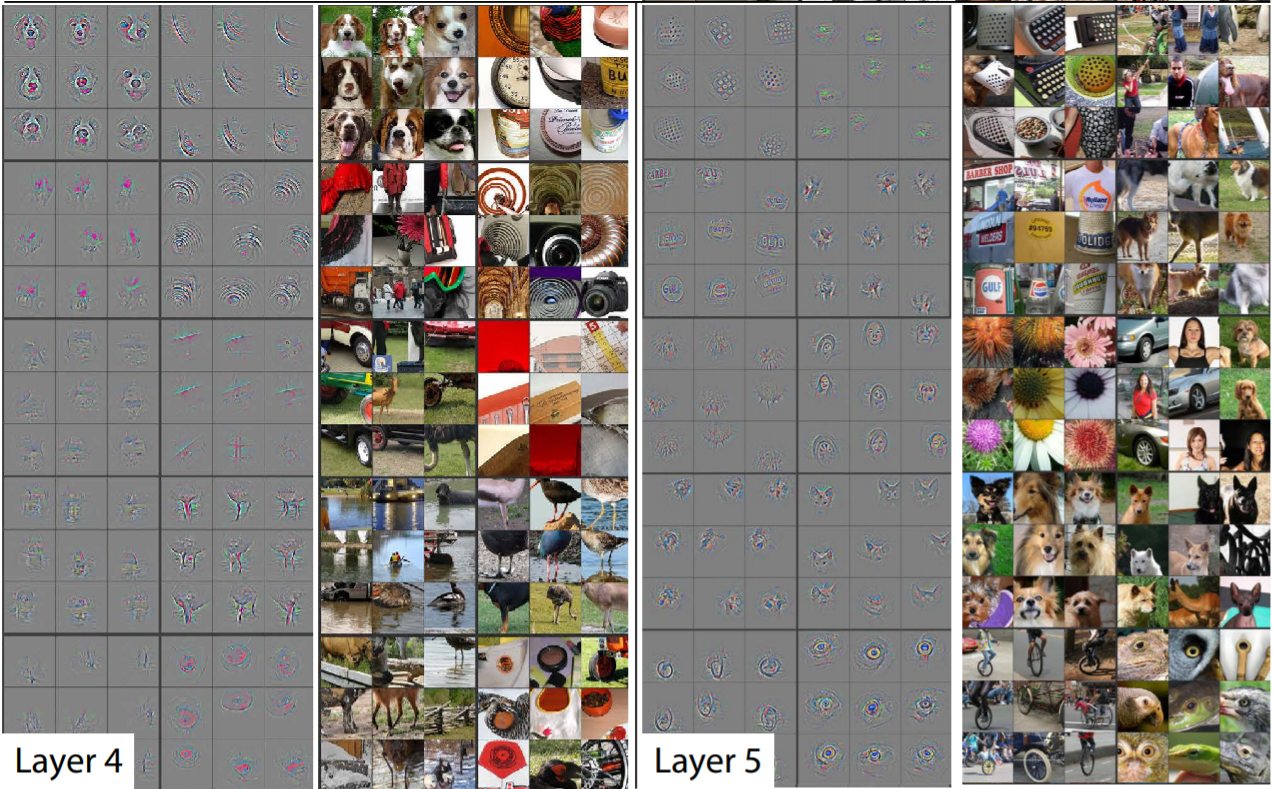
Convolution is an operation done to extract features from the images as these features will be used by the network to learn about a particular image.In the case of a dog image,the feature could be the shape of a nose or the shape of an eye which will help the network later to identify an image as a dog.
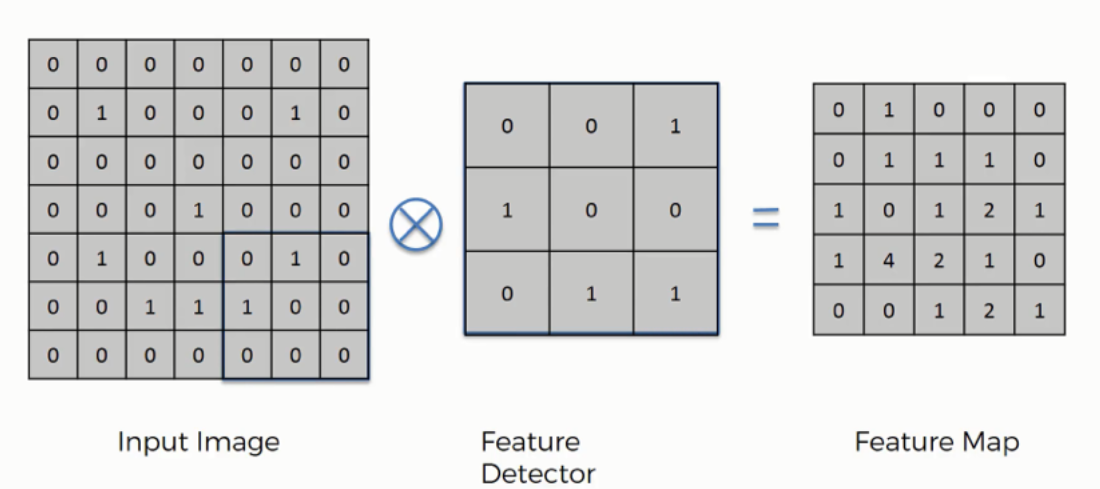
Convolution operation is performed with the help of the following three elements:
1.Input Image- The image to convolve on
2.Feature Detector/Kernel/Filter- They are the bunch of numbers in a matrix form intended to extract features from an image.They can be 1dimensional ,2-dimensional or 3-dimensional
3.Feature Map/Activation Map- The resultant of the convolution operation performed between image and feature detector gives a Feature Map.


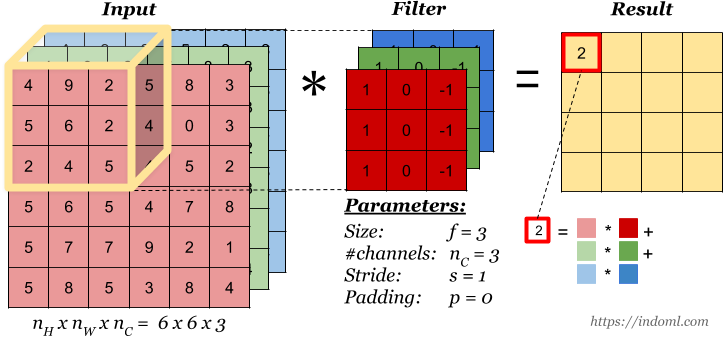
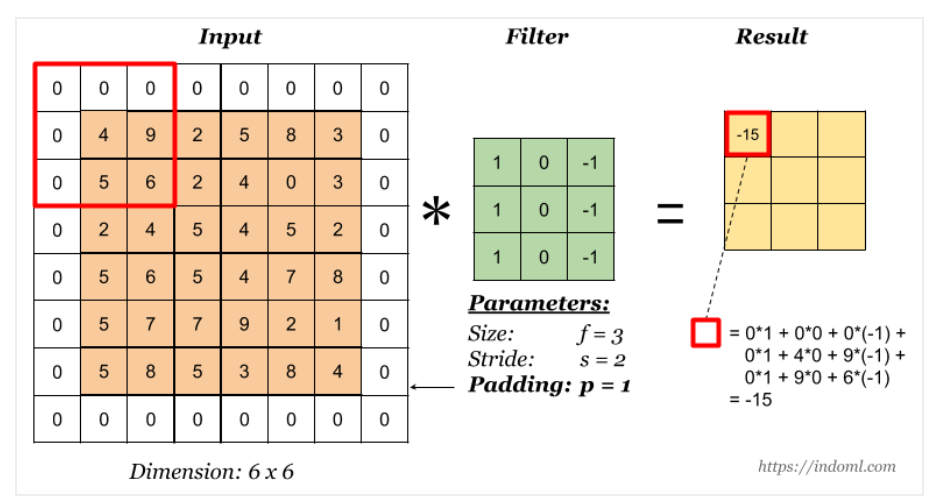
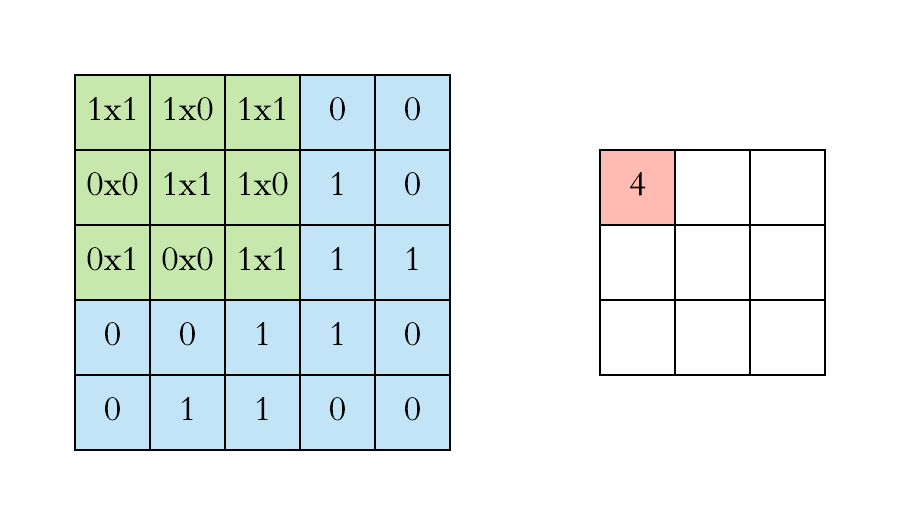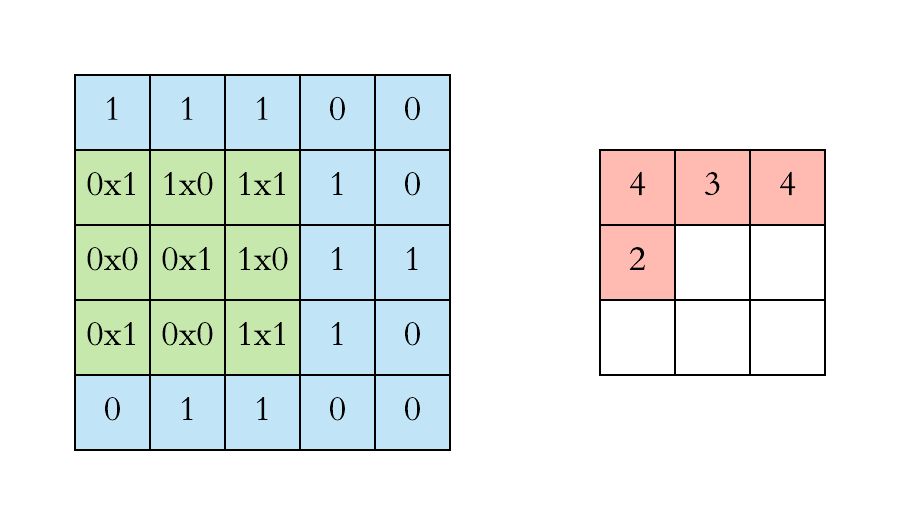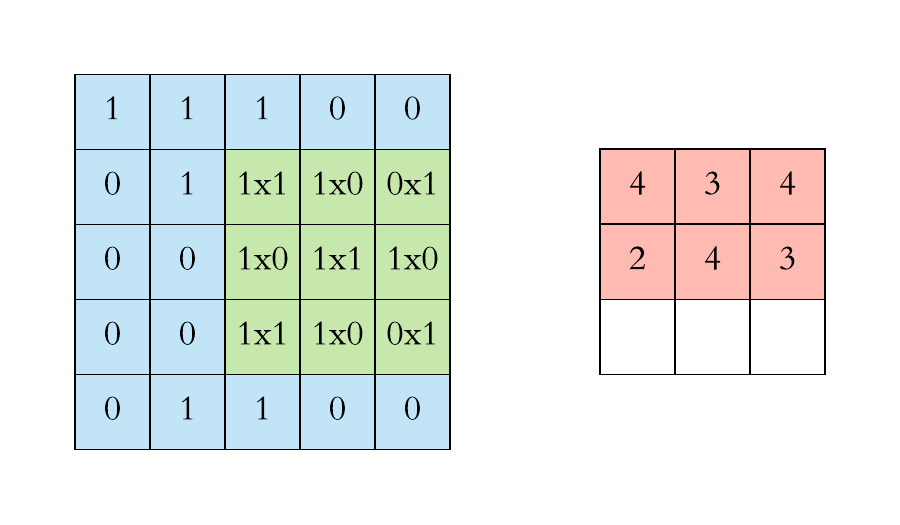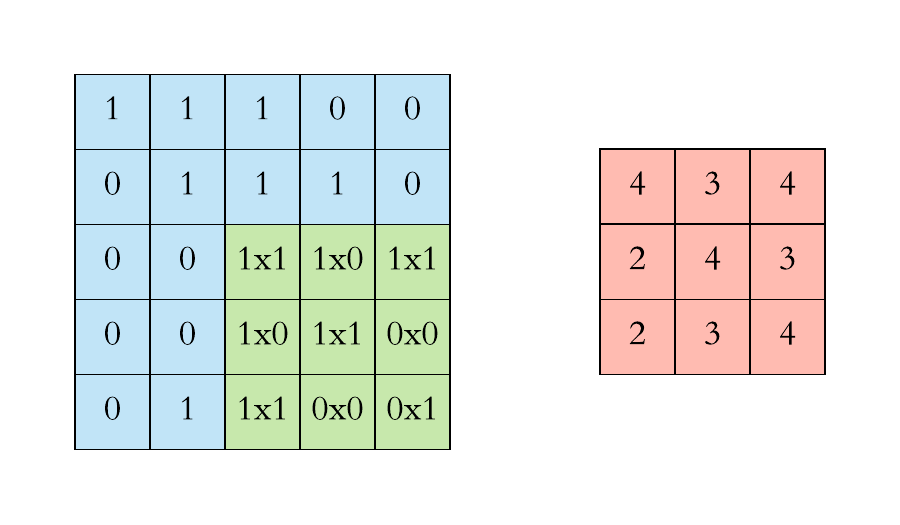
Convolution Operation
Another way to look at it
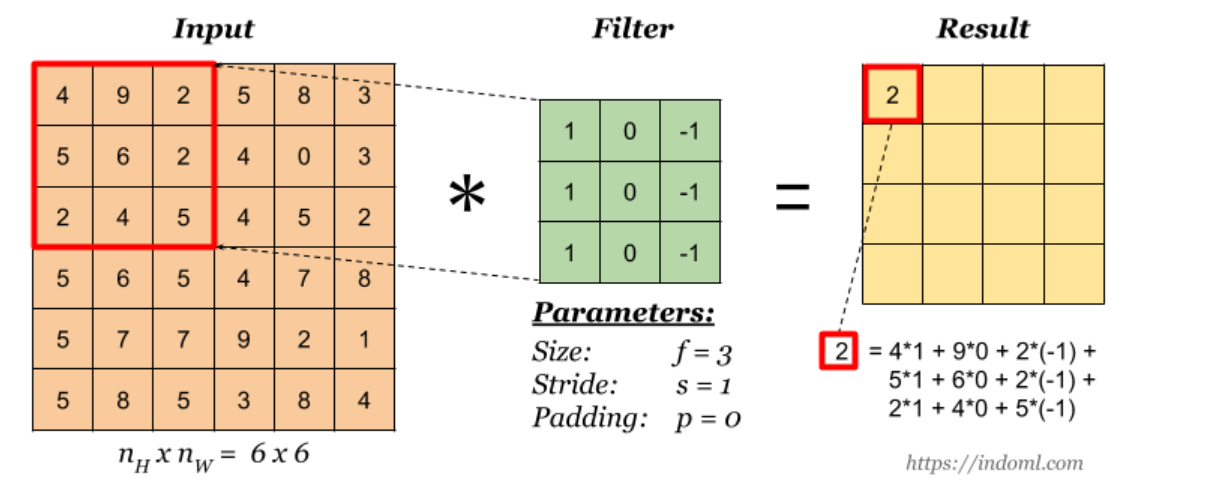
Let say we have an input of $6 x 6$ and a filter size $3 x 3$
Feature map is of size $4 x 4$
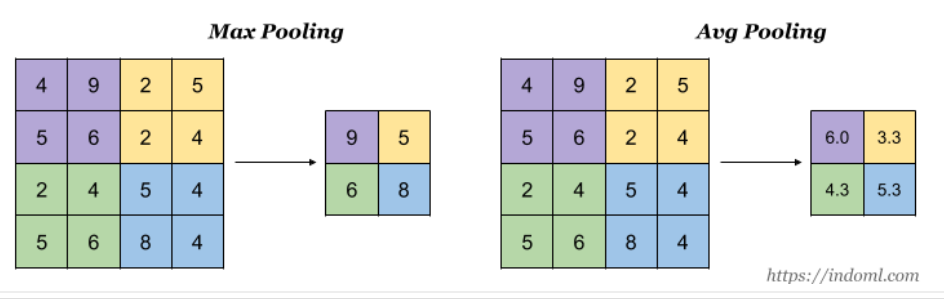
Pooling
Why we do Pooling?
The idea of max pooling is:
- to reduce the size of representation in such a way that we carry along those features which speaks louder in the image
- to lower the number of parameters to be computed,speeding the computation
- to make some of the features that detects significant things a bit more robust.
Analogy that I like to draw
A good analogy to draw here would be to look into the history of shapes of pyramid.
The Greek pyramid is the one without max pooling whereas the Mesopotamian pyramid is with max pooling involved where we are loosing more information but making our network simpler than the other one.
But don't we end up loosing information by max pooling?
Yes we do but the question we need to ask is how much information we can afford to loose without impacting much on the model prediction.
Perhaps the criteria to choose how often(after how many convolutions) and at what part of the network (at the beginning or at the mid or at the end of the network) to use max pooling depends completely on what this network is being used for.
For eg:
- Cats vs Dogs
- Identify the age of a person
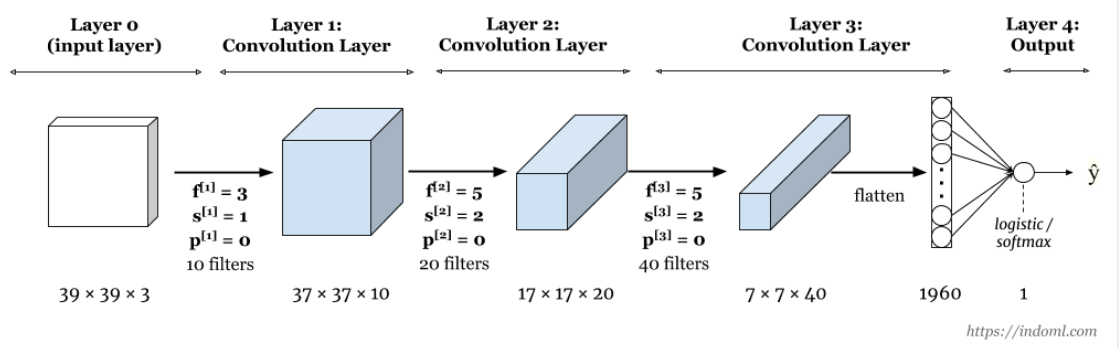
General Representation-Updated
Including Padding and Stride
$$Input Image [n(h)*n(w)*n(c)]-Filter-[f(h)*f(w)*n(c)],n(c')--Feature Map--[((n-f+2p)/s+1)*((n-f+2p)/s+1)*n(c')]$$
$n(h)$-height of the image
$n(w)$-width of the image
$n(c)$-number of channel in an image
$f(h)$-height of the filter
$f(w)$-width of the filter
$f(c')$-no of the filter
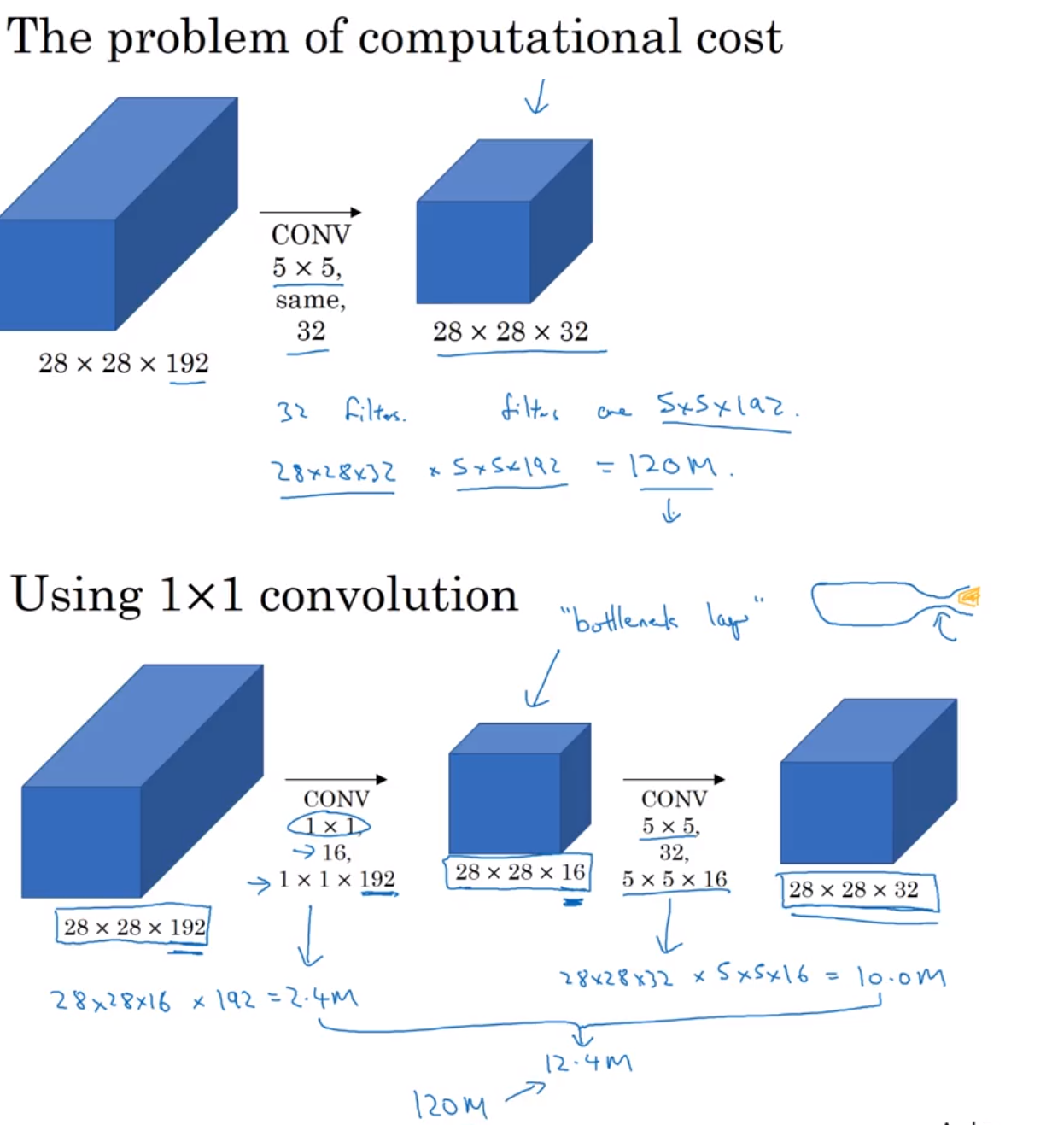
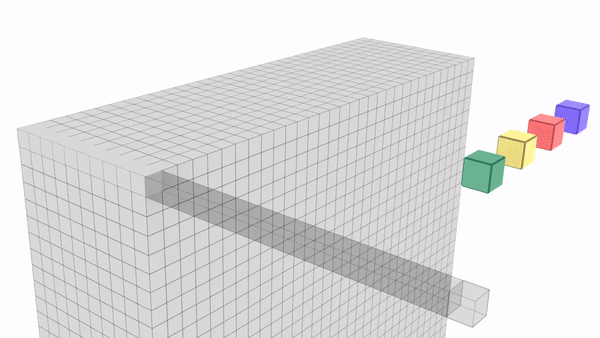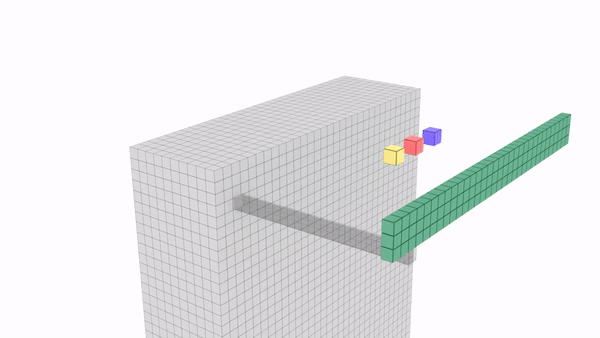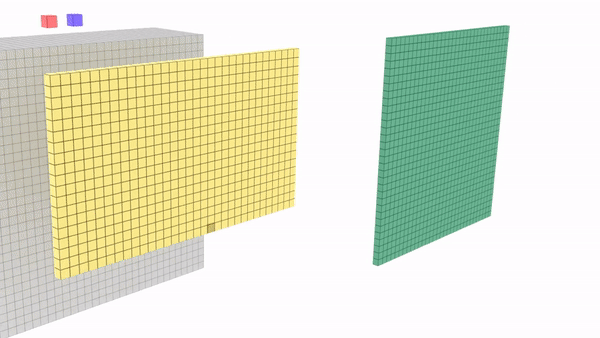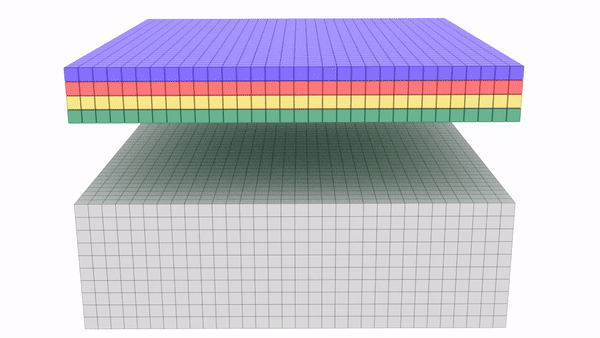
1 x 1 Convolution
At first,the idea of using 1x1 filter seems to not make sense as 1x1 convolution is just multiplying by numbers.We will not be learning any feature here.
But wait... What if we have a layer with dimension 32x32x196,here 196 is the number of channels and we want to do convolution
So 1x1x192 convolution will do the work of dimensionality reduction by looking at each of the 196 different positions and it will do the element wise product and give out one number.Using multiple such filters say 32 will give 32 variations of this number.
 Why do we use 1x1 filter
Why do we use 1x1 filter
-
1x 1 filter can help in shrinking the number of channels or increasing the number of channels without changing the height and width of the layer.
-
It adds nonlinearity in the network which is useful in some of the architectures like Inception network.
References
Convolution
Max Pool
Standford Slides
Standford Blog
An intuitive guide to Convolutional Neural Networks
Convolutional Neural Networks
Understanding of Convolutional Neural Network
Receptive Feild Calculation
Understanding Convolution in Deep Learning
Visualize Image Kernel
Visualizing and Understanding Convolution Networks